Lukujen näyttäminen tasossa (määritelmä)

2024 Kirjoittaja: Leah Sherlock | [email protected]. Viimeksi muokattu: 2023-12-17 05:35

Kyky esittää oikein erilaisia muotoja arkin, kankaan ja minkä tahansa muun pinnan tasossa on melko merkittävä taito. Ja ennen kaikkea se on tärkeä sekä taiteilijoille: maalareille, kuvanveistäjille, graafikoille, suunnittelijoille (sisustustilojen ja arkkitehtonisen ympäristön) että tiedemiehille: matemaatikoille, fyysikoille, suunnittelijoille, keksijöille.

Mutta on myös tärkeää, että ihminen, joka on kaukana näistä sfääreistä, oppii hahmottamaan ja näyttämään ympäröivää maailmaa oikein. Tämä auttaa ymmärtämään sen monipuolisuutta paljon syvemmin. Jos sinulla ei ole riittävää käsitystä siitä, kuinka tämä tehdään oikein, et todennäköisesti onnistu minkään keksinnön projektissa, kuvassa tai piirustuksessa. Tämä taito on siis tärkeä sekä yksinkertaisten, jokapäiväisten tehtävien ratkaisemisessa että sellaisissa, joilla on globaali, universaali merkitys.

Hieman historiaa

Ihmiset ovat muinaisista ajoista lähtien yrittäneet kuvata sitä, mitä he näkivät ympärillään: muita ihmisiä, joitakin noiden aikojen alkukantaisia rakennuksia, hämmästyttävän kaunista kasvi- ja eläinmaailmaa, majesteettisia vuoria ja yksinkertaisesti tavaroita, kodin esineitä. Eli maailma kaikessa monimuotoisuudessaan ja loistossaan.

Mutta silloin heillä ei vielä ollut aavistustakaan, kuinka se voitaisiin tehdä tarkasti ja asiantuntevasti niin, että erilaisten kolmiulotteisten kohteiden näyttäminen tasossa oli todella realistista, elävää. Henkilöllä ei ollut tarvittavia tietoja eikä myöskään erityisiä taitoja, paitsi ehkä alkeellisimmat.

Aiemmissa lähteissä sanotaan, että maailman ensimmäinen maalaus koostui vain yhdestä viivasta, joka kulki auringon seinälle heittämän henkilön varjoa pitkin. Eli luonto itse ehdotti, mihin suuntaan tähän asiaan kannattaa siirtyä oikean ratkaisun etsimiseksi.

Ja tämä kysymys huolestutti tuon ajan miestä myös tästä syystä: hän ei halunnut vain ihailla tilavaa elävää siluettia, niin sanotusti alkuperäistä, vaan halusi vangita tila-objektin tasoon. Ja hän teki tämän, jotta hän voisi tällä tavalla joko sisustaa kotinsa tai hänelle pyhän paikan tai ottaa kuvan sisältävän nippun mukaansa ja siirtää sitä mihin tahansa etäisyyteen.

Kuvion geometria

Ja mitä tahansa sanotkin, mutta vuosia kului, vuosisatoja kului, ja jotenkin sivilisaation kehittyessä ihmiset oppivat vähitellen näyttämään monimutkaisia hahmoja kaksiulotteisessa avaruudessa, toisin sanoen tasossa. Vasta nyt kuvattujen esineiden kokojen ja mittasuhteiden tarkkuus alkoi vaikuttaa hyvin likimääräiseltä.

Mutta kysymys siitä, kuinka oikein hahmon näyttäminen tasossa ja kuinka paljon ne vastaavat alkuperäisten esineiden tilavuutta, tuli kerran hyvin tärkeäksi. Jollain tapaa uusi tiede nimeltägeometria. Tarkemmin sanottuna sen leikkaus on kuvaavaa geometriaa.

Tässä hän vain tutkii muotoja ja tasoja, viivoja ja pisteitä sekä niiden suhdetta toisiinsa - sekä kolmiulotteisessa että kaksiulotteisessa avaruudessa.

Muuntostavat

Kuvataiteen tärkeä piirre on hahmojen näyttäminen kuvatasolla. Loppujen lopuksi tämä on kolmiulotteisten tilaobjektien vangitsemista kaksiulotteisuudessa. Nimittäin: kompleksi on muutettava yksinkertaiseksi, eli objekti, jolla on pituus, leveys, korkeus, on siirrettävä tasolle.

Ja kuvaileva geometria tekee tällaisia "siirtymiä" joidenkin menetelmien ansiosta. Niitä on yhteensä noin kuusi. Tässä on kolme tärkeintä ja suosituinta ympäri maailmaa:

• perspektiivi (kun kuvattu kohde poistetaan avaruudessa);
• ortogonaalinen projektio (rinnakkaisprojektio, jossa säteet ovat kohtisuorassa tasoon nähden);
• vino projektio (rinnakkaisprojektio, jossa säteet ovat vinossa suhteessa tasoon).

Kuvattu kohde näkyy melko selkeästi aksonometrisessa projektiossa (johon sisältyy ortogonaalinen ja vino). Mutta se projisoidaan selkeimmin ja aidoimmin, kun se esitetään perspektiivissä. Ja juuri yllä olevat menetelmät ratkaisevat suurelta osin kysymyksen lukujen esittämisestä tasossa.

Perspektiivi

Perspective ottaa kunniallisimman paikan muiden imagomenetelmien joukossa. Koska ihmisen silmäkuten kameran linssi, se näkee ympäröivän tilan samalla tavalla. Asiat, jotka ovat kauempana havaitsijasta, näyttävät kooltaan pienempiä ja joskus paljon pienempiä kuin ollessaan lähellä.

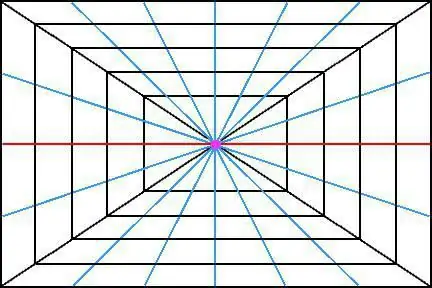
Ota esimerkiksi kuva kuutiosta avaruudessa. Jos itse asiassa kaikki sen reunat ovat yhdensuuntaiset toistensa kanssa, niin kun katsot tätä kohdetta etäisyydellä, saattaa vaikuttaa siltä, että reunat lähentyvät (tai niiden pitäisi lähentyä) yhdessä pisteessä. Ja mikä mielenkiintoisinta, niiden ei pitäisi vain supistua yhteen pisteeseen, vaan niillä on oltava yksi leikkauspiste.

Renessanssin mestareiden Albrecht Dürerin, Piero Della Francescan, Andrea Mantegnan, Leon Batista Albertin ansiosta moderni maalaus tietää, mitä suora lineaarinen perspektiivi on, kuinka määrittää horisontin korkeus ja katoamispisteet.

Ja maailmankuulu nero - Leonardo da Vinci - väitti ensin ilmaperspektiivin käsitteen. Tämä sisältää muutoksen kohteen värissä, sävyssä, muutoksia sen kontrastiominaisuuksissa (pienenee kohteen liikkuessa pois).

Ortografinen projektio

Ortogonaalista kutsutaan yhdensuuntaista projektiota, joka on suunnattu suoralle viivalle, joka on kohtisuorassa tasoon nähden. Sen soveltamisprosessissa kohteen ääriviivojen mitat pysyvät muuttumattomina. Eli objekti näytetään ilman vääristymiä.

Projisoitu kolmiulotteinen kohde on ikään kuin jaettu kolmeen näkymään: sivulta, edestä ja ylhäältä. Ja kun katsot tätä kaikkea samanaikaisesti, voit lisätäesitys siitä, miltä esine näyttää tilavuudessa. Samanaikaisesti hahmon mitat pysyvät ennallaan sekä kolmiulotteisessa että kaksiulotteisessa kuvassa.

Viisto projektio

Tämä projektio on jaettu useisiin alalajeihin, nimittäin:

• isometrinen näkymä;
• dimetrinen projektio;
• trimetrinen projektio.

Isometrialla on vääristymäkertoimet kaikilla kolmella akselilla (pituus, leveys, korkeus). Toisin sanoen pareittain otettujen akselien väliset kulmat ovat 120 astetta. Dimetrisessä vääristymät kahdella akselilla ovat yhtä suuret ja kolmannella erilainen. Trimetrisessä projektiossa kaikki vääristymäkertoimet (eli kaikilla kolmella akselilla) ovat erilaisia.

Kiertomuodot

Kun suorakulmainen kolmio pyörii toisen jalan akselia pitkin, sen kolmas sivu (hypotenuusa) kuvaa uutta kuviota, jota kutsutaan kartioksi. Ja jos käännät suorakulmiota (neliötä) sen yhtä sivua pitkin, saat sylinterin. Kun puoliympyrä pyörii, pallo tulee ulos.

Tästä seuraa, että pyörittämällä tasoa jotakin akselia pitkin, saadaan ns. kiertoluvut.

Näillä kuvilla on pyörimisakseli. Niiden ulkonäkö tasossa riippuu niiden sijainnista suhteessa silmien tasoon. Esimerkiksi sylinterin ylä- ja alasivut ovat olennaisesti ympyröitä. Ja jos katsot niitä tasossa, ne näyttävät ellipsiltä.

Mutta tehtävästä tulee vielä vaikeampi, jos näytössätilahahmot tasossa, niillä on k alteva akseli. Tässä tapauksessa on tärkeää, että pyörimiskappaleiden ääriviivat ovat yhtä kaukana jälkimmäisen akselista.

Hieman chiaroscurosta

Chiaroscurolla on tärkeä rooli hahmojen esittämisessä lentokoneessa. Koska kuvatun kohteen tilavuus ei synny vain linjojen vuoksi, vaan myös valon ja varjon oikeasta jakautumisesta sen sivuille. Ja sitten se näyttää melko tilav alta kaksiulotteisen pinnan tasossa.

Näin ollen kuvien näyttäminen tasossa, niiden koon määrittäminen, vaaleuden ja tummien pisteiden oikean peiton ominaisuudet ovat täysin mahdollisia yllä olevien menetelmien ansiosta. Ja mikä tärkeintä, nämä ovat todella käytännössä todistettuja menetelmiä, joita aikamme johtavat asiantuntijat käyttävät.